Las lluvias de "estrellas" (que ni son estrellas ni llueven) sin "tontás"

Uno de los "grandes" acontecimientos astronómicos de cada verano son las "Perseidas", que suelen llenar minutos de programación de los informativos que no tienen nada mejor que contar (bueno, sí lo tienen pero con el calor... ¡que pereza!) Un poquito cansados de los tópicos y tontás que se llegan a decir hemos pensado en aclarar las cosas que, en realidad, son bastante sencillas.

¡Mira! ¡Una estrella fugaz!  - Que no!!! Que no es eso!

Cada verano pasa lo mismo: alguien mira al cielo, ve un fogonazo cruzar la noche y grita emocionado “¡Una estrella se ha caído!”. Bueno, pues no. Ni estrella, ni caída, ni fugaz en el sentido de que se vaya a ningún sitio.

¿Qué demonios es entonces?

Una estrella fugaz es, en realidad, un meteoro. Palabra que viene del griego meteoros, que significa “alto en el aire”. Muy científico todo.

Un meteoro es básicamente un trocito de roca o polvo espacial (llámalo meteoroide cuando está flotando por ahí) que entra en la atmósfera de la Tierra a toda leche (de 11 a 72 kilómetros por segundo).

Meteoro o Estrella Fugaz (NASA)

Cuando esto ocurre, la fricción no quema literalmente el fragmento por dentro, sino que calienta el aire a su alrededor hasta temperaturas de 3.000 °C o más, eso es la mitad que la superficie del Sol. Ese aire se ioniza, forma un plasma y emite luz. Por eso la “colita luminosa” no es el meteoro ardiendo como un fósforo: es la atmósfera brillando de puro susto.

¿Llegan ardiendo hasta el suelo?

No, esto es mito nivel leyenda urbana. La mayoría de meteoroides son tan pequeños que se vaporizan completamente a decenas de kilómetros de altura. El aire hace de freno y horno a la vez: ¡se desintegran antes de llegar!

Si un trozo es lo bastante grande como para resistir, se va enfriando muy rápido al final de su trayectoria. Un meteorito que aterriza no llega ardiendo, lo normal es que esté frío o templado. Lo que más se calienta con la fricción es el aire, no el propio material.

Así que, precisemos, que al fin y al cabo esto es Ciencia.

• Meteoroide: La roca o partícula que está flotando en el espacio hasta que se ve atraído por La Tierra u otro astro.
• Meteoro: El destello luminoso en la atmósfera provocado por la entrada del meteoroide a toda velocidad.
• Meteorito: Lo que llega al suelo, si algo llega.

Meteoroide, meteoro o meteorito?
Excelente gráfico del Observatorio Astronómico de Córdoba

A veces, un meteoroide es grande (pongamos un melón, o una pelota de baloncesto). Eso genera un bólido: un destello que puede iluminar más que la Luna llena; a veces pueden provocar un "boom" sónico y dejar retumbando a medio pueblo. Estos sí pueden dejar fragmentos que busquen acogida en tu jardín. Pero tranquilos, es rarísimo, por eso luego cuestan tanto en internet.

¿Por qué brillan de colores?

¿Has notado que algunas estrellas fugaces son blancas, otras azuladas o verdosas? No es decoración navideña interplanetaria, es pura química. La roca (o la mota de polvo) trae consigo metales y minerales que se excitan (y se ionizan) con la brutalidad de la entrada atmosférica. Resultado: fuegos artificiales gratis.

• Verde: mucho magnesio.
• Naranja-amarillo: sodio, como en las farolas de antes.
• Rojo: oxígeno y nitrógeno de la atmósfera.
• Violeta: Calcio, sobre todo.
• Blancos-azulados: mucho hierro.

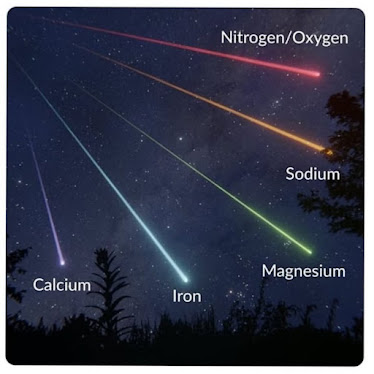Lección gratis de Química Interplanetaria

Además, la velocidad influye: cuanto más rápido entra, más energía para ionizar, más brillo y más color. El tamaño también es muy importante aquí, cuanto mayor sea el meteoroide mejor se apreciará el color del meteoro.

Entonces, ¿qué narices son las Perseidas?

Las Perseidas son la lluvia de meteoros más famosa del verano. Cada agosto, la Tierra cruza la estela de polvo que deja el cometa Swift-Tuttle en su viaje alrededor del Sol. Ese polvillo cósmico (del tamaño de granos de arena) se encuentra con nuestra atmósfera y se lanza hacia la Tierra a casi 60 Km/s… voilà: cielo tachonado de rayas luminosas.

Las Perseidas se llaman así porque parecen venir de la constelación de Perseo, pero no tienen nada que ver con Perseo, solo es un punto de perspectiva. Una noche muy oscura y con suerte se pueden observar hasta 100 perseidas por hora.

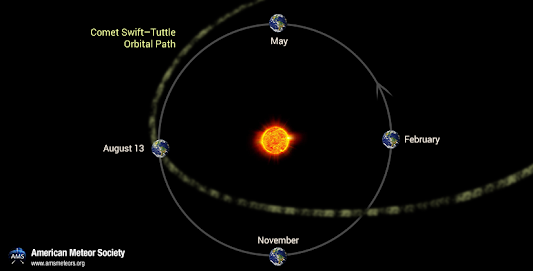El cometa Swift-Tuttle lo va dejando todo perdido de polvo, pero La Tierra
mantiene muy limpita su propia órbita atrayendo todo lo que encuentra a su paso,
y nos da un espectáculo a mediados de Agosto.

Una buena tasa, pero no la mayor; este honor corresponde probablemente a las Gemínidas, unas 150 por hora en las noches del 13 al 15 de diciembre. Pero claro, quien es el o la valiente que se va a las eras a observar las Gemínidas en una noche de diciembre?

¿Cómo verlas bien sin llorar de decepción?

1. Fuera del pueblo: nada de farolas, ni pantallas encendidas.
2. Manta o tumbona: cuello relajado, sin tortícolis.
3. Mirar al cielo, no al móvil. Las Perseidas te avisan gratis, no por notificación push.
4. Paciencia: ver una decente cada minuto es buen promedio.
5. Hora punta: mejor de medianoche a amanecer.

Gráfico para localizar las Perseidas el 13 de Agosto
La Luna estará todavía crecidita, así que podría ocultar el brillo de muchos meteoros

Un último deseo

Así que, la próxima vez que veas “una estrella fugaz”, recuerda: no es una estrella, no se está cayendo y no va a encender la barbacoa si aterriza. Es polvo cósmico, fuego atmosférico y un recordatorio de que, incluso una partícula minúscula, a la velocidad adecuada, puede arrancarte un “¡guau!”

En resumen:

• Las estrellas fugaces no son estrellas.
• Lo que brilla es el aire, no la roca.
• El color te cuenta su composición.
• La mayoría se desintegran mucho antes de llegar al suelo.
• Si llegan al suelo puede hacer pupa según su tamaño, pero ya está frío.
• La próxima vez que pidas un deseo, piensa que estás confiando tu suerte a un grano de polvo espacial a 60 km/s.

Y así, cada agosto, la Tierra barre su porción de polvo cósmico… y nos regala uno de los espectáculos más humildes, y más bonitos, del cielo.

Hasta Septiembre... si es que volvemos 😉

“¡Estamos en gravedad cero!” — Este... deja que te diga algo.

Seguro que has oído esa frase en películas, series o incluso en vídeos de astronautas o cosmonautas flotando en el espacio. Y sí, ahí están, moviéndose como plumas en el aire… o mejor dicho, en el "vacío". Entonces, ¿es verdad que están en “gravedad cero”? Pues no, no lo es.

Vamos a dejarlo claro desde el principio: la gravedad está en todas partes. Incluso donde parece que no está.

¿Qué es eso de la “gravedad cero”?

Lo que normalmente llamamos “gravedad cero” es un nombre algo tramposo. Deberíamos hablar de microgravedad (valores muy bajos de gravedad) o, mucho mejor, de ingravidez (sensación de ausencia de gravedad). Suena menos espectacular, pero es mucho más preciso y, sobre todo, cierto.

Imagina que estás en una montaña rusa justo en el momento en que comienza a caer. Por un instante, sientes que tu cuerpo se levanta del asiento: estás cayendo. No porque no haya gravedad, sino porque tú y el asiento caéis al mismo ritmo. Esa es la sensación que tienen los astronautas… ¡pero todo el tiempo!

Están en caída libre constante. Orbitan la Tierra, sí, pero cayendo hacia ella sin llegar a tocarla, porque se mueven tan rápido de forma tangencial que la curva de su caída coincide con la curvatura del planeta. Como decía Perelman, están en caída constante pero no aciertan a chocar contra la Tierra 😉 Por cierto que la velocidad tangencial que necesita la nave para seguir sin "acertar" se puede calcular como: 

Entonces… ¿por qué flotan?

Porque están en un entorno donde todo está cayendo a la vez: ellos, su nave, los objetos dentro… no hay “suelo” que los detenga. Y como nada frena esa caída, da la impresión de que flotan. Pero la gravedad sigue ahí, tirando de ellos con fuerza: aproximadamente un 90 % de la que sentirían en tierra.

No flotan porque la gravedad haya desaparecido, sino porque todo su entorno cae junto con ellos.

La tripulación 67 de la ISS jugando con la ingravidez
(pero bajo gravedad, de otra forma saldrían despedidos de la Tierra y nunca hubieran vuelto)

Otra forma de ver que algo no cuadra: si los cosmonautas, que están como mucho a 450 km de la Tierra, no experimentaran gravedad, ¿cómo es posible que la Luna, que está a más de 384.000 kilómetros, quede atrapada por la fuerza gravitatoria terrestre? En efecto, la Luna experimenta la fuerza de gravedad de la Tierra… y nuestras naves espaciales en órbita, mucho más.

¿Todavía te cuesta imaginarlo? Prueba con esto:

Imagina que estás en un ascensor y, de repente, se rompe el cable (¡esperamos que nunca te pase!). Mientras caes, si sueltas una pelota, no caerá al suelo del ascensor: quedará flotando frente a ti, acompañándote en la caída. Da la impresión de que no hay gravedad… justo cuando estás a punto de estrellarte contra el suelo.

El inolvidable Stephen Hawking experimentando Ingravidez  en el avión de Zero-G.
Básicamente un enorme ascensor al que se le corta el cable pero aterriza en lugar de estrellarse.

Eso es ingravidez: la gravedad sigue ahí, pero como todo cae igual… no se nota.

¿Y en el espacio profundo?

Aún lejos de la Tierra, la gravedad no desaparece. Lo que ocurre es que se debilita con la distancia. Pero incluso entre planetas, estrellas o galaxias, la gravedad nunca es cero. Es como una telaraña gigante que lo conecta todo. Cuanto más lejos estés de una masa, más débil será la fuerza, pero seguirá existiendo.

Por eso las sondas espaciales pueden ser desviadas por planetas, o viajar siguiendo trayectorias curvas: están “aprovechando” la gravedad de esos cuerpos.

La confusión del término

Decir “gravedad cero” suena bien, pero es un atajo lingüístico. Un poco como decir que “el Sol sale por el Este”, cuando sabemos que no es el Sol el que se mueve. Es una forma sencilla de expresar algo más complejo… pero vale la pena entender la diferencia para no caer en falsas concepciones que luego serán difíciles de eliminar de nuestro entendimiento sobre la naturaleza.

Fotograma de la película Gravity, una de las más respetuosas con
las leyes físicas sobre Gravedad.

Así que en la próxima película o historia de ciencia ficción, cuando hablen de gravedad cero o de máquinas que anulan la gravedad, acuérdate del ascensor cayendo. Y piensa que, si realmente no hubiera gravedad, ni el satélite ni los astronautas estarían ahí arriba: habrían salido disparados en línea recta, como un tornillo suelto en el espacio. Y entonces podrás decir: Este... deja que te diga algo.

¿Está el espacio realmente vacío?

Spoiler: no. Y además, da un poco de miedito.

Hay cosas que damos por hechas, que parecen evidentes; lo que pasa es que no hay nada evidente en la Naturaleza. Recordemos humildemente que nuestro cerebro ha evolucionado para ser capaces de cooperar con otros miembros de la especie en conseguir comida y no ser comida de otros depredadores. Y con esa única herramienta, con su grandeza, pero también con sus grandes limitaciones, nos hemos lanzado a comprender el Cosmos. Estaba claro que alguna sorpresa nos íbamos a llevar.

Uno de nuestros antecesores volviendo a la cueva después
 de un duro día cazando mamuts y huyendo de los dientes de sable,
 mientras medita sobre el Vacío Cósmico.

Por ejemplo, es "evidente" que cuando miramos al cielo entre estrella y estrella, entre planeta y planeta, lo que hay es... nada. El vacío. El gran silencio cósmico. Y es razonable pensarlo: si no hay aire, ni luz, ni sonido, si nada nos empuja ni nos detiene, si un astronauta se suelta y sigue flotando sin rozar nada en su camino... eso debe de ser el vacío, ¿no?

Pues no; pero un NO a lo bestia.

El vacío clásico: ese malentendido.

Cuando decimos “vacío” solemos imaginar un espacio completamente desprovisto de todo. Como una caja de la que se extrae todo el aire, de forma que no quede "nada" dentro. Pero en Física, incluso en la Física Clásica, eso es un ideal que no se alcanza jamás. Ni en el laboratorio más avanzado, ni en el rincón más solitario del espacio interestelar.

El “vacío” del espacio entre planetas, o entre estrellas, está lleno... de casi nada. Pero ese “casi” es muy importante; es lo que llamamos Espacios Interplanetario e Interestelar.

Por término medio, en un solo centímetro cúbico de ese vacío espacial puede haber generalmente uno o dos átomos, casi siempre de hidrógeno y un poco de helio, viajando solos como almas en pena desde el mismísimo Big Bang sin haber tenido la suerte de formar parte de alguna estrella o cualquier otro cuerpo celeste.

Large Hadron Collider (CERN)
su interior es el lugar más vacío de la Tierra

También hay polvo cósmico (particulas de tamaño inferior a 100 micrómetros), partículas de alta energía, fotones, neutrinos, campos electromagnéticos y gravitatorios que lo atraviesan todo... y eso sin contar lo que todavía no entendemos bien.

Seguramente el mayor vacío logrado en la Tierra es el que existe en el interior del acelerador de partículas LHC (Large Hadron Collider) del CERN; y es del orden de 1,000 átomos por centímetro cúbico. Es decir, una superpoblación de partículas, comparado con el espacio interestelar.

Si nos alejamos de nuestra galaxia y miramos el llamado Espacio Intergaláctico mediremos "vacíos" mucho mayores, con un átomo de hidrógeno por metro cúbico de media, al borde de la "nada".

El vacío cuántico: la nada que lo es todo

Cuando entramos en el terreno de la Física Cuántica, (la física fundamental que trata de dar la respuesta más profunda a cualquiera de nuestras preguntas) la idea del Vacío da un triple salto mortal sin red. Ya no osamos hablar de “ausencia de cosas”, sino de el estado de menor energía posible del espacio.

Y resulta que ese estado mínimo no es, ni de lejos, un mar de tranquilidad. De hecho, es un hervidero invisible. El vacío cuántico está lleno de lo que llamamos fluctuaciones: pares de partículas y antipartículas que aparecen y desaparecen constantemente, como si el universo se aburriera y necesitara improvisar.

Simulación matemática del Vacío Cuántico:
Pares de partículas y antipartículas en constante estado
de creación y aniquilación.

Este fenómeno no es una elucubración científica, ni un arreglo matemático que explique algo sin poder demostrarlo con experimentos: ¡se ha medido! 

El efecto Casimir, algo predicho por la teoría cuántica de campos, consiste en que, si separamos dos placas metálicas una distancia muy pequeña comparada con su tamaño, entre ellos aparecerá una fuerza de carácter atractivo (no gravitatoria) debido a las diferencias en las fluctuaciones del vacío cuántico entre el espacio interior y exterior de las placas. El Vacío ejerce "presión" sobre las placas y las acerca. El efecto Casimir ha sido comprobado sin ningún género de dudas.

Ilustración que pretende explicar el efecto Casimir:
presión que ejercen las fluctuaciones del vacío exterior
frente a las fluctuaciones del vacío interior.

Así que el vacío, desde el punto de vista cuántico, no está vacío. Está lleno de posibilidades. Y de hecho, según algunas teorías, todo lo que vemos, toda la materia real, es una especie de excitación del vacío. Un pequeño cosquilleo que se sale del habitual equilibrio de la nada.

Energía del vacío: más misterio

Y aún más raro: ese vacío “lleno de nada” podría ser responsable de la expansión acelerada del universo. Sí, eso que, a falta de un término mejor porque no tenemos ni idea de lo que es, llamamos energía oscura. Algo que, por cierto, representa la mayor parte del contenido energético del cosmos. Y viene, posiblemente, de esa energía latente del vacío.

Así que puede que el espacio entre las galaxias, aparentemente desierto, sea en realidad el motor silencioso que empuja todo a separarse de todo, cada vez más rápido. Una nada que no deja de hacer cosas.

This amazing and expanding Universe, como decían los Monty Python.
 Resulta que es el Vacío el que lo hace expandirse

Así que no, el espacio no está vacío. Ni siquiera en sus rincones más oscuros. Es un océano de energía sutil, un campo lleno de vibraciones, de fuerzas invisibles, de partículas fantasma que aparecen y desaparecen antes de que puedas notarlas. Lo que llamamos “nada”... el universo lo usa como lienzo para pintar todo lo demás.

Por otro lado, ¿no es maravilloso pensar que la Nada simplemente no puede existir? A algunos seres mitológicos seguro que no les hace tanta gracia 😉

Las preguntas de Iria (episodio 2) ¿Por qué la gente de Australia no se cae?

- "Papá, si la Tierra es redonda… ¿la gente en Australia o en Sudamérica vive boca abajo? ¿Y no se caen?", preguntó Iria mientras giraba el globo terráqueo e imaginaba a los habitantes del Hemisferio Sur “colgando” boca abajo o directamente cayendo al espacio infinito. 

¿Sabías que esta pregunta la hacen muchas personas, grandes y pequeñas? Tiene todo el sentido: si imaginamos la Tierra como una bola flotando en el espacio, y dado que nosotros estamos en el Hemisferio Norte (que es, desde luego, la parte de "arriba"), parecería que la gente que está “abajo” debería vivir boca abajo... o caer al vacío. Pero, ¿qué pasa realmente? Vamos a descubrirlo.

¿Qué es ‘abajo’?

Lo primero que debemos entender es que “abajo” no es una dirección universal que apunta siempre al mismo lugar en el espacio. Para cada persona sobre nuestro planeta, “abajo” es la dirección hacia el centro de la Tierra, porque es hacia donde actúa la fuerza(*) de la gravedad. Igual que para cada persona "arriba" significa la dirección que apunta a lo que está encima de su cabeza.

La gravedad es una fuerza atractiva que la Tierra ejerce sobre todos los objetos, dirigiéndolos hacia su centro de masas. Por eso, sin importar en qué punto del planeta estemos, “abajo” será siempre hacia ese centro.

Simple pero eficaz gráfico de lo que significa "Arriba" y "Abajo"
el ‘abajo’ es según tu ‘debajo’ y el suelo se encarga del resto.

Ni nosotros ni los habitantes del Hemisferio Sur sentimos que estamos “boca abajo” porque nuestro cuerpo siempre sabe dónde está el “abajo” real: hacia el centro de la Tierra. Desde que nacemos, la gravedad tira de nosotros hacia el suelo, así que nos “pegamos” a la superficie, sin importar en qué parte del planeta estemos.

No estamos en el borde de algo que se termina; estamos sobre la superficie de una esfera enorme. En realidad, estamos “cayendo” hacia el centro de la Tierra todo el tiempo, pero el suelo nos detiene y nos sostiene para que no nos hundamos.

Un detalle curioso es que la gravedad actúa con una fuerza ligeramente distinta en nuestros pies y en nuestra cabeza, porque están a diferentes distancias del centro de la Tierra. Esa diferencia, aunque pequeña, se siente como una tensión que produce cansancio muscular. Por eso, cuando nos tumbamos, reducimos esa diferencia y le damos un descanso al cuerpo.

Un posible origen de la confusión

Cuando representamos la Tierra en una esfera no podemos evitar confundir los conceptos "Hemisferio Norte" con "arriba" y "Hemisferio Sur" con "abajo"; pero esto es totalmente incorrecto. Como hemos dicho, el concepto físico, es decir real, de “abajo” no depende de dónde esté el norte o el sur en el mapa, sino de dónde estamos nosotros con respecto al centro del planeta. Por eso, para alguien en Australia, su “abajo” es justo hacia adentro, al centro, igual que para nosotros aquí.

Map Mundi en proyección Gall-Peters.
Una representación más proporcional de las áreas, con el Sur arriba.

¿Y ya puestos, qué significan Norte y Sur?

Ya hemos aclarado que decir que un Hemisferio de la Tierra, o de cualquier planeta, está "arriba" es sencillamente absurdo. Aun así llamamos a cada hemisferio de un planeta, separados por su ecuador, "Norte" y "Sur". ¿Cómo elegimos cuál es cuál? 

Cuando hablamos del polo norte y el polo sur de un planeta, nos referimos a los dos puntos donde su eje de rotación (esa línea invisible alrededor de la cual gira sobre sí mismo) atraviesa la superficie. El polo norte es, por convención, el extremo desde el que el planeta parece girar en sentido contrario a las agujas del reloj, y el polo sur, el extremo opuesto. Es una definición práctica, no una verdad del Universo, que funciona aunque el planeta esté al revés, como Venus... pero eso ya lo contaremos otro día.

Para pensar y reír un poco (Gracias Quino, por todo)

¿Conoces a Mafalda? En una famosa tira se da cuenta de que los argentinos viven "del revés", con todos los problemas que eso supone. 

Tras varias tiras, en las que todos los maravillosos personajes de Quino se la pasan boca abajo discutiendo sobre  el tema, Mafalda encuentra la solución perfecta dándole la vuelta al globo.

Y es que, en realidad, todos tenemos nuestro propio “arriba” y “abajo” según dónde estemos. Así que, la próxima vez que veas a Australia o Argentina “del revés” en un globo terráqueo, recuerda: ¡ellos también te ven a ti igual de patas arriba!

(*) Nota para puristas

Sí, ya sabemos que la gravedad posiblemente no sea una fuerza, sino una manifestación de la curvatura del espacio-tiempo causada por la concentración de energía. Reconocido queda para los tikismikis.

El Universo a la fuga: Líneas espectrales y Corrimiento al Rojo

Hay luces que nos hablan en lenguajes que la humanidad ha sabido descifrar: las estrellas y galaxias emiten radiación que, al descomponerse en las diferentes longitudes de onda que la forman (por ejemplo en un prisma), revela una firma única: las líneas espectrales descubiertas por Fraunhofer. Son como códigos de barras cósmicos. Y cuando esas líneas se desplazan —hacia el rojo o hacia el violeta— de donde se supone que deben estar, nos cuentan una historia de movimiento, velocidad, y expansión.

🌈 ¿Por qué aparecen líneas en los espectros?

De manera muy básica: cuando un átomo recibe energía, sus electrones saltan a niveles (capas electrónicas) más altos, más alejados del núcleo. Al volver a su nivel original, emiten energía en forma de luz con longitudes de onda muy específicas. Ese patrón da lugar a líneas de emisión.

Por el contrario, si una fuente de luz atraviesa un gas frío, ese gas absorbe ciertas frecuencias, dejando líneas oscuras en el espectro continuo. Son las líneas de absorción.

Espectros de emisión del Sodio, Hidrógeno, Calcio y Mercurio
comparados con el espectro continuo de luz visible

Ambas son fundamentales: con ellas identificamos los elementos químicos del laboratorio o de las estrellas y galaxias, sin importar cuán lejanas estén. Fueron Kirchhoff y Bunsen los que descubrieron esta asociación entre posición de las líneas y el elemento químico que las produce. De hecho, gracias a las líneas espectrales se descubrió Helio en el Sol (de ahí su nombre, por cierto), antes que en la Tierra.

🟥 Corrimiento al rojo y al violeta

Cuando las líneas espectrales se desplazan respecto a su posición de reposo, hablamos de:

• Corrimiento al rojo: las líneas se mueven hacia el extremo rojo del espectro: longitudes de onda más largas, menos frecuencia.

Espectro de absorción del Hidrógeno en los siguientes casos (de arriba a abajo)
a) En reposo (laboratorio) b) Alejándose a 3,000 Km/s c) Alejándose a 30,000 Km/s

• Corrimiento al azul o violeta: las líneas se desplazan hacia el extremo violeta del espectro: longitudes más cortas, más frecuencia.

Espectro de absorción del Hidrógeno en los siguientes casos (de arriba a abajo)
a) En reposo (laboratorio) b) Acercándose a 3,000 Km/s c) Acercándose a 30,000 Km/s

Este fenómeno puede tener tres causas:

Efecto Doppler: Si una fuente de emisión se aleja, su luz se "estira", si se acerca, se "comprime". Por tanto podemos deducir que las galaxias que presentan corrimiento al rojo se alejan de nosotros y las que presentan corrimiento azul se acercan, como Andrómeda, debido a su propio movimiento por el Cosmos.

El efecto Doppler, aplicado a las ondas mecánicas en el aire que llamamos sonido, es algo que todos apreciamos con facilidad cuando, por ejemplo, se acerca una motocicleta a gran velocidad: cuando se acerca a nosotros el sonido se vuelve más agudo, las ondas de sonido se "aprietan", su longitud disminuye; pero cuando se aleja, las ondas se van estirando, se alarga su longitud, y de ahí un sonido más grave. 

Corrimiento gravitacional: La luz pierde energía al escapar de campos gravitatorios intensos. Ya hablaremos de este tema en el futuro.

Expansión o Contracción del espacio-tiempo: No es que las galaxias viajen por el espacio alejándose o acercándose, que también lo hacen... sino que sería el mismísimo espacio el que se expande o contrae, y con él, la luz misma.

El Universo en expansión, representación ilustrativa
(Science Photo Library)

Spoiler😉: Dado que la gran mayoría de las galaxias se alejan de nosotros, y lo hacen más deprisa cuando más lejos están, provocando evidentes corrimientos al rojo, llegamos a la conclusión de que es precisamente la Expansión del Universo el motivo fundamental del corrimiento de las líneas (aunque los otros dos también contribuyen). El Universo está expandiéndose mientras lees este artículo.

🌌 Friedmann, Lemaître y el universo en expansión

Aunque solemos asociar la expansión del universo con Hubble y su famosa fórmula V = H x d (Velocidad de la galaxia respecto a la Tierra igual a la Constante de Hubble multiplicada por la distancia hasta la galaxia), la idea no le pertenece. Fue el científico soviético Alexander Friedmann, en 1922, quien derivó de las ecuaciones de Einstein que un universo estático era imposible: debía expandirse o contraerse, y todo eso solo con un cuaderno, un lápiz y un cerebro capaz de entender a Einstein y precisarle unos detalles. Su trabajo fue ignorado, como también lo fue el del sacerdote y astrónomo belga Georges Lemaître, quien en 1927 llegó a conclusiones similares y propuso lo que hoy conocemos como la teoría del Big Bang.

Es cierto que fue Hubble quien observó experimentalmente que las galaxias parecían alejarse más cuanto más lejos estaban, pero ni siquiera esto lo hizo solo. Detrás de sus datos estaban los cálculos y mediciones realizadas por mujeres como Henrietta Swan Leavitt, Milton Humason y otras "calculadoras" invisibles a la historia oficial de la Ciencia.

En definitiva, las líneas espectrales desplazadas al rojo eran la huella de esa expansión predicha por Friedmann y Lemaître.

🧭 ¿Por qué importa todo esto?

Porque las líneas espectrales nos permiten medir distancias cósmicas, calcular velocidades de galaxias, reconstruir la historia misma del universo y proyectar su destino... casi nah. Y todo gracias a unos arañazos de luz.

Científicas, Matemáticas y Astrónomas: Sofja Kovalevskaya

Hoy presentamos, en nuestra serie Científicas, Matemáticas y Astrónomas, a Sofja Kovalevskaya, matemática.

Sofja Vasilyevna Kovalevskaya (Софья Васильевна Ковалевская), durante mucho tiempo conocida en Occidente como Kovalevsky —cuando aún se ignoraba que en ruso los apellidos tienen forma femenina— nació en Moscú en enero de 1850. Era hija de Vasily Vasilievich Krukovsky, oficial de artillería y descendiente del rey de Hungría Matías I, que llegaría a ser comandante del Arsenal del Kremlin, y de Elizaveta Fyodorovna Schubert, alemana y nieta de Theodor Schubert, matemático y astrónomo de la Academia de San Petersburgo. Ella era mucho más culta y educada que su marido.

Sofja Vasilyevna Kovalevskaya

Curiosamente, Vasily era hijo de polaco y rusa, así que Sofja solo era rusa por una cuarta parte de su sangre y siempre sintió una fuerte afinidad con los movimientos revolucionarios alemán y polaco del siglo XIX.

Sus primeros contactos con las matemáticas llegaron por caminos insólitos: por un lado, su padre había estudiado cálculo en el ejército, como parte de su formación artillera. Una anécdota cuenta que, en ausencia de papel pintado, empapeló una habitación con litografías de conferencias de Ostrogradsky, y Sofja pasó horas de su infancia escudriñando aquellas fórmulas incomprensibles. Por otro lado, adoraba a su tío Pyotr Vasilievich, un autodidacta con gran afición por las matemáticas.

Pronto empezó a destacar por su capacidad de autoestudio y su facilidad para explicar conceptos matemáticos complejos. Algunos amigos de la familia sugirieron entonces a Vasily que permitiera que Sofja recibiera una formación matemática adecuada. Durante su juventud, se sintió fuertemente atraída por Fyodor Dostoevsky, aunque parece que el escritor mostró más interés por su hermana mayor, Anna.

La ley rusa no permitía a una mujer tener pasaporte propio; para estudiar en el extranjero, necesitaba el permiso de su padre o un marido. Vasily se oponía a que Sofja y Anna salieran del país, así que la única solución pasaba por un matrimonio estratégico. Si una de las dos hermanas se casaba, el esposo podría legalmente tomar también a la cuñada bajo su protección. Así encontraron a Vladimir Kovalevski, más tarde famoso paleontólogo, quien, plenamente consciente de las razones de Sofja, accedió a casarse con ella en septiembre de 1868. Años después, la pareja se convirtió en un matrimonio de hecho, y en 1878 nació su hija, también llamada Sofja.

En mayo de 1869, Sofja y Vladimir llegaron a Heidelberg, donde ella estudió física con Gustav Kirchhoff, fisiología con Hermann von Helmholtz y matemáticas con Leo Königsberger y Paul DuBois-Reymond. En 1870 intentó ingresar en la Universidad de Berlín para estudiar con Karl Weierstrass. El matemático, sorprendido por la audacia de una mujer que quería entrar en su aula, decidió actuar con justicia: le entregó varios problemas. Sofja los resolvió todos, y Weierstrass inició el proceso de admisión. Sin embargo, la administración de la universidad se negó en rotundo. Weierstrass decidió entonces darle clases particulares durante cuatro años.

Mujeres defendiendo la Comuna de París

En 1871, Sofja y su marido se vieron envueltos en una aventura política. Su hermana Anna había viajado a París y se había unido a la Comuna, el breve gobierno revolucionario que dirigió la ciudad durante la ocupación prusiana. Sofja y Vladimir lograron entrar en la París sitiada y ayudaron en los hospitales. Cuando la Comuna fue derrotada, huyeron con Anna a Londres. Anna se quedó allí, fue acogida por Karl Marx y más tarde tradujo sus obras al ruso.

En 1874, con el apoyo de Weierstrass, Sofja obtuvo el grado de Doctor en Matemáticas y Maestro en Bellas Artes por la Universidad de Göttingen, gracias a sus trabajos sobre ecuaciones diferenciales y su aplicación al estudio de los anillos de Saturno. Fue el primer doctorado en matemáticas otorgado a una mujer. Ese mismo año regresó a Rusia y trató de conseguir un puesto en la Universidad de San Petersburgo, sin éxito. Tal vez por decepción, abandonó por unos años la investigación y se centró en su afición por la literatura.

Matemáticamente, estaba aislada: no solo por ser mujer, sino por ser discípula de Weierstrass, referente del análisis matemático puro, mientras que en Rusia predominaba el análisis aplicado. La única excepción fue el maestro Chebyshev, que sí valoró su trabajo.

En 1880, tras varios fracasos económicos que afectaron gravemente la salud mental de Vladimir, Sofja decidió volver a las matemáticas. Se trasladó a Moscú, pero fue rechazada nuevamente por la universidad. Viajó a Berlín y luego a París en busca de un puesto como profesora. Finalmente, en 1884, fue aceptada como profesora en la Universidad de Estocolmo. Era la tercera mujer en lograr ese grado académico.

Peonza de Kovalevskaya

Desde su nuevo puesto, completó sus estudios sobre dinámica de la rotación de sólidos, aplicando la teoría de funciones abelianas. Por estos trabajos recibió el Premio de la Academia de Ciencias de París en 1888 y, un año después, el Premio de la Academia Sueca de Ciencias, antecesor del Nobel.

En 1889, fue finalmente reconocida en su país como la primera mujer nombrada miembro correspondiente de la Academia de Ciencias de San Petersburgo, gracias a la iniciativa de Chebyshev.

Lamentablemente, apenas tuvo tiempo de disfrutar ese reconocimiento: falleció de gripe y neumonía en febrero de 1891, a los 41 años. Sofja está enterrada en el cementerio de Norra begravningsplatsen, junto a otros notables suecos.

Esta semblanza de Sofja Kovalevskaya nació años atrás en otro lugar digital, el Menschliche Walhalla, un proyecto de memoria humanista que hoy duerme en silencio. Reaparece aquí revisada, como artículo 40 de este blog, como un acto de gratitud.

Cuando la Tierra era el centro del Universo… y tenía sentido que lo fuera

Cuando Ptolomeo salvó las apariencias

Ptolomeo muy orgulloso con sus epiciclos,
 deferentes y, sobre todo, sus ecuantes

Hoy nadie duda de que la Tierra gira alrededor del Sol, y que el Sol, a su vez, no es más que una estrella entre miles de millones. Pero hubo un tiempo —un tiempo largo— en que imaginar esto habría parecido absurdo. En ese tiempo vivió Claudio Ptolomeo, en el siglo II de nuestra era, y fue él quien escribió la obra astronómica más influyente de la Antigüedad: el Almagesto. El manual definitivo para explicar el cielo... aunque fuera a base de 'rodeos'.

No era fácil ser astrónomo entonces. No había telescopios, ni relojes precisos, ni datos fiables. Solo estaban los cielos, el ojo humano… y mucha paciencia. Ptolomeo, como casi todos sus predecesores, asumía algo que parecía evidente: que la Tierra estaba quieta en el centro del cosmos. Y con esa premisa, intentó que las cuentas cuadraran.

Spoiler: lo consiguió. Pero a un precio.

El arte de ajustar un modelo a martillazos

Las observaciones del cielo tenían un problema: los planetas no se movían de forma sencilla. A veces avanzaban, a veces retrocedían (lo que hoy llamamos movimiento retrógrado). Si la Tierra estaba quieta, ¿cómo explicar eso?

La solución no era cambiar la hipótesis de partida —¡ni pensarlo!—, sino ajustar el modelo para que encajara. Así nació la arquitectura de epiciclos y deferentes: cada planeta giraba en un pequeño círculo (epiciclo), cuyo centro a su vez giraba en otro círculo mayor (deferente) alrededor de la Tierra.

Era como dibujar con un espirógrafo cósmico. Y funcionaba. No a la perfección, pero sí lo bastante bien como para predecir posiciones planetarias sin volverse completamente loco... aunque por momentos debieron rozarlo. Ptolomeo pulió y mejoró este modelo heredado, muy posiblemente de Hiparco, (a quien ya dedicaremos su artículo) añadiendo elementos como el “ecuante” (un punto excéntrico desde el que el movimiento parecía uniforme) para que las observaciones encajaran mejor. Si quieres jugar con el concepto aquí tienes un modelo geocéntrico ptolemáico. 

De sphaera mundi, de Johannes de Sacrobosco. Una versión medieval (c.1230) del Almagesto de Ptolomeo. La fotografía es de una edición impresa de 1550

Desde nuestra perspectiva actual, esto parece un galimatías. Pero hay que verlo como lo que era: un intento monumental por hacer que el modelo coincidiera con lo que se veía en el cielo. No era física, era geometría aplicada con talento y tenacidad. Y durante más de mil años, fue el sistema de referencia para entender el universo.

Antes de menospreciar el esfuerzo de Ptolomeo deberíamos recordar al mismísimo Newton. También él se empeño en encontrar un orden perfecto en el Sistema Solar que no existía y negó las explicaciones de Leibniz como vimos en otro artículo. O qué decir de los físicos actuales modificando modelos matemáticos cada vez más complejos para explicar fenómenos cuánticos o la materia oscura con tal de no bajarse de sus concepciones de salida...

Cuando el centro depende de dónde mires

Hoy decimos que Ptolomeo estaba equivocado. Pero, si nos ponemos quisquillosos, hay que matizar: su modelo era complejo y feo, sí; menos útil que el heliocéntrico, sin duda; pero físicamente, no era incorrecto.

Porque en el fondo, todo movimiento es relativo. Puedes describir el sistema solar desde cualquier punto: desde el Sol, desde la Tierra… incluso desde Júpiter. Lo que cambia es la complejidad de las cuentas. Decir que el Sol está en el centro es elegir un marco de referencia más sencillo y coherente con la dinámica gravitacional. Pero nadie te impide poner la Tierra en el centro… solo que necesitarás muchos más círculos y correcciones para explicarlo todo.

¿Heliocentrismo o Geocentrismo? Cuestión de gustos... o de salud mental

Ptolomeo eligió el centro más lógico para él. No porque fuera terco o ciego, sino porque desde su marco cultural y tecnológico, no tenía razones de peso para hacerlo de otro modo. Y además, su modelo funcionaba. Mal que bien, pero funcionaba.

En otras palabras, la Tierra era el centro del universo... si uno decidía que lo fuera. Esta idea, si bien astronómicamente errónea, era físicamente tan válida como cualquier otra.

Ptolomeo no fue el único. Otros astrónomos, como Hiparco, también trataron de ajustar las órbitas planetarias a la teoría geocéntrica. Pero fue el modelo de Ptolomeo el que perduró durante siglos, gracias a las traducciones árabes, hasta que las ideas de Copérnico finalmente lo desafiarían.

¿Por qué importa todo esto?

Porque nos recuerda que la ciencia no avanza por iluminación divina, sino por ensayo, error, y una voluntad tremenda de que las cosas encajen aunque sea a martillazos. Ptolomeo no descubrió que la Tierra se movía pero nos legó un sistema ordenado y coherente, un método de cálculo preciso y, sin quererlo, el indicio más claro de que el geocentrismo era cada vez más insostenible.

Universo Ptolemaico,
Cornipolitanus Chronographia 1537
Un universo perfecto... o no?

Sin embargo, el principal problema del Geocentrismo de Ptolomeo no fue su incapacidad para explicar fenómenos o su inexactitud, sino su instrumentalización, siglos después, por la nueva religión imperante en Occidente, el cristianismo. Los teólogos cristianos empuñaron el modelo de Ptolomeo como prueba de la supuesta inmutabilidad del universo y de la posición privilegiada de la Tierra y del ser humano (aunque no precisamente de toda la Humanidad) en el centro de la creación divina. La Iglesia trató por todos los medios a su alcance, y no pocos, de mantener el geocentrismo como una doctrina inapelable - Galileo y Bruno podrían contarnos detalles sobre esto - en lugar de tratarlo como lo que era: un modelo geométrico válido hasta cierto punto y desechable una vez se supera con datos y evidencias.

Pero su caída, con Iglesia o sin ella, era inevitable. Cuanto más complicado era hacer que el sistema funcionara, más evidente se hacía que tal vez la hipótesis de partida no era la mejor. Y así, Copérnico, Kepler y Galileo tomarían el relevo… y le darían la vuelta al sistema.

No olvidemos, sin embargo, que todo gira en torno a lo mismo: elegir un buen punto de vista, lo que en física se llama "marco de referencia". Y que la Tierra no sea el centro del universo no significa que no pueda serlo, si elegimos contar las cosas desde aquí. Después de todo, desde donde miras, tú también estás en el centro.

Medir el Cosmos con una regla y un compás (II): Aristarco

Cuando un griego midió el cielo a ojo… y casi acertó

En una época sin telescopios, sin satélites y sí, sin Google Maps, un griego se plantó bajo el cielo armado con un compás, un poco de geometría y mucha audacia. Se llamaba Aristarco de Samos y vivió en el siglo III antes de nuestra era. Y aunque hoy no lo sepa casi nadie, fue el primero que se atrevió a calcular el tamaño y la distancia del Sol y de la Luna... y a decir, ¡siglos antes de Copérnico! que la Tierra gira alrededor del Sol.

¿Y cómo lo hizo? Con una idea brillante y unos cálculos que hoy diríamos “a ojo”… pero un ojo entrenado en ciencia, que ya quisiéramos muchos.

Midiendo ángulos con la Luna a medio gas

Imagina que es de noche y ves la Luna en cuarto creciente, la mitad iluminada y la mitad en sombra. Ese momento no solo es bonito: es una gran oportunidad geométrica. Si la mitad de la Luna está iluminada, eso significa que la línea que separa luz y sombra —el terminador— está justo perpendicular a la dirección al Sol. Es decir, el ángulo en la Luna, entre el Sol y la Tierra, es de 90°.

Aristarco comprendió que, si en ese momento podía medir el ángulo entre el Sol y la Luna en el cielo (visto desde la Tierra), podía construir un triángulo rectángulo con vértices en la Tierra, la Luna y el Sol. Con un poco de trigonometría (lo que hoy llamaríamos una tangente), la relación entre las distancias queda determinada.

Aristarco intentó medir el ángulo α para determinar completamente el triángulo entre los tres astros y así poder deducir las distancias relativas del Sol y Luna hasta la Tierra

Él midió —a ojo, sin instrumentos ópticos— un ángulo α de unos 87°, lo que implica que el Sol está unas 20 veces más lejos que la Luna. La cifra real es unas 400 veces, pero no perdamos la perspectiva: ¡medir un ángulo en el cielo, a simple vista, con solo una regla y compás, es un logro impresionante! Más aún si ahora sabemos que el ángulo real es de 89,85°, casi imposible de distinguir a simple vista de un ángulo recto.

El tamaño de la Luna y el Sol: comparando sombras

Con ese dato de las distancias, Aristarco pasó al siguiente paso lógico: calcular los tamaños relativos. Ya sabía que la Luna y el Sol se ven del mismo tamaño aparente (ambos cubren unos 0,5 grados en el cielo), así que si uno está 20 veces más lejos, debe ser unas 20 veces más grande.

En un Eclipse Solar se aprecia con claridad que los diámetros aparentes de Sol y Luna, vistos desde la Tierra son casi iguales

Pero además, hizo otro razonamiento: observó los eclipses lunares y dedujo que, cuando la Tierra proyecta su sombra sobre la Luna, podemos medir el tiempo que nuestro satélite tarda en cruzar la zona de Umbra y estimar así la relación del radio de esta sombra con respecto al radio de la Luna y, con un poco de trigonometría básica, llegar a la relación que conecta el tamaño de la Tierra con el del Sol y el de la Luna y las distancias de la Tierra-Sol y Tierra-Luna. 

 

Así, combinando observaciones de eclipses, mediciones angulares y una medida de tiempo dedujo:

• Que la Luna estaba a unas 60 veces el radio de la Tierra (valor real: ~60,3 radios terrestres).
• Que el diámetro de la Luna era aproximadamente un tercio del de la Tierra (el valor real es ~0,27 veces). No está nada mal.
• Que el Sol debía ser unas siete veces mayor en diámetro que la Tierra (en realidad es 109 veces mayor, pero aquí la imprecisión viene de su ángulo de 87°).
• Y sobre todo, que el Sol, al ser tan inmenso, probablemente debería ser el centro del sistema formado por los tres astros.

Es decir, lo importante no es si acertó, sino que tuvo la idea correcta y las herramientas mentales para alcanzarla.

Para completar sus cálculos con datos concretos y no solo relativos, a Aristarco le hubiera hecho falta conocer, por ejemplo, el tamaño de la Tierra. Con ese dato habría podido calcular las distancias entre los tres astros y el tamaño del Sol y la Luna; pero Eratóstenes, unos 35 años más joven que Aristarco, todavía no había hecho el cálculo que relatamos en el artículo anterior.

¿Y si no somos el centro?

Aquí llega la genialidad: Aristarco no se conformó con calcular distancias y tamaños relativos. Se atrevió a decir que el modelo tradicional, con la Tierra inmóvil en el centro del universo, no encajaba con lo que estaba descubriendo. Si el Sol es más grande y está tan lejos, ¿no tiene más sentido que la Tierra gire a su alrededor?

Aristarco, compás en mano, dispuesto a medirse
con Apolo… sin más ayuda que Euclides.

Y así lo propuso en, tal vez, el primer modelo heliocéntrico. En él, la Tierra gira sobre sí misma y da vueltas al Sol. Su modelo no se conserva, pero sabemos de él gracias a Arquímedes, que lo cita en su obra El Arenario.

Fue el primer griego (que sepamos) que osó decirlo… y el último durante casi dos mil años. No es que lo refutaran: simplemente lo ignoraron. Aristóteles y Ptolomeo seguirían dominando el pensamiento durante siglos, con sus esferas celestes y su cosmos geocéntrico bien ordenado. La intuición de Aristarco quedó relegada a los márgenes de la historia de la Ciencia.

Pero renació: en el siglo XVI Copérnico la rescató, y aunque no la copió tal cual, sí que conocía el antecedente de Aristarco. Esa semilla antigua germinó y cambió el mundo.

Epílogo: medir el cielo con geometría y valor

Hoy sabemos que la Luna está a unos 384.000 km, y el Sol a casi 150 millones. Pero fue Aristarco quien, armado de una regla y un compás, se atrevió a medir distancias astronómicas cuando la Ciencia aún estaba en pañales.

La próxima vez que veas la Luna a medio iluminar, recuerda: ahí, justo en ese ángulo, empezó una revolución. No con telescopios, ni con matemáticas avanzadas, sino solo con ojos atentos, algo de sombra y... la pasión por saber.

Medir el Cosmos con una regla y un compás (I): Eratóstenes

En esta pequeña serie de artículos os vamos a contar como los antiguos griegos pudieron medir, o al menos estimar, las dimensiones de la Tierra, la Luna y el Sol, y las distancias entre ellos. No vamos a respetar el orden en que ocurrieron los descubrimientos que os vamos a contar, porque preferimos ponerlos en el orden lógico en que nos pueden contestar, precisamente, a estas preguntas: ¿Cuánto miden la Tierra, la Luna y el Sol? y ¿A qué distancia está nuestro planeta de la Luna y el Sol? Todo ello desde luego sin ningún avance moderno, ni siquiera un pobre telescopio. Disponemos, como los antiguos griegos solamente de un par de reglas, un porta-ángulos y, ojalá tambien tengamos como ellos, curiosidad e inteligencia.

Empezamos por el final: Eratóstenes midiendo el mundo

En una bulliciosa Alejandría del siglo III a.e.c., entre rollos de papiro y disputas filosóficas, un hombre llamado Eratóstenes tenía una curiosidad insaciable. Director de la Gran Biblioteca, matemático, geógrafo y, por lo que sabemos, el tipo al que acudir cuando querías medir cosas imposibles, Eratóstenes escuchó un día una historia intrigante: en la ciudad de Siena, en el sur del Egipto Helénico (actual Asuán), el día del Solsticio de verano al mediodía el Sol iluminaba el fondo de los pozos y los obeliscos no proyectaban sombra alguna.

Eratóstenes recibiendo la noticia sobre la sombra de los obeliscos en Siena
- Pero ¿qué me estás contando hombre?
- Como te lo digo Eratós, colega; ni rastro de sombra al mediodía el día del Solsticio.
- Vaya, vaya, vaya... y si...

Aquí es donde la mayoría de la gente habría dicho "qué curioso" y seguido con su vida. Pero no Eratóstenes. A la sazón, ya había medido en unos 23º 54' el ángulo del plano de la eclíptica (su valor real es 23º 17'); recordemos que el ángulo de la eclíptica es la inclinación del plano en el que la Tierra orbita alrededor del Sol con respecto al ecuador celeste; así que Eratóstentes llegó rápidamente a la conclusión de que Siena debería tener precisamente esa latitud (recordemos que latitud es distancia en grados hasta el ecuador terrestre). Y se pregunto: ¿y si midiera la sombra en Alejandría exactamente al mismo tiempo? 

Así lo hizo y encontró que en Alejandría, al mediodía del Solsticio de verano, los objetos sí proyectaban sombra. Algo no cuadraba. Eratóstenes razonó que el Sol debía estar tan alejado de la Tierra que sus rayos llegaban de forma paralela a ambas ciudades y, asumiendo que ambas tuvieran la misma longitud (distancia en grados a un meridiano elegido arbitrariamente), la sombra de los obeliscos en Alejandría serviría para calcular la diferencia en latitud entre ambas ciudades y de ahí el tamaño de la Tierra, así sin anestesia.

Con su mente matemática ya disparada, Eratóstenes midió el ángulo de la sombra proyectada en Alejandría y encontró que era aproximadamente de 7 grados y 12 minutos de arco. Si la Tierra fuera plana, no habría diferencia en la inclinación de las sombras. Pero ya que era esférica, como todo griego culto sabía, la diferencia indicaba cuánto se había curvado su superficie entre ambas ciudades.

Eratóstenes midió el ángulo A 7º 12', o bien midió la sombra y la altura del obelisco, que tanto da.
El ángulo A es idéntico al ángulo B, por tanto sabiendo B y midiendo la distancia entre
ambas ciudades, d, sabremos el tamaño de la Tierra.

Tras los datos, el cálculo.

Ahora venía el siguiente paso: estimar el tamaño de la Tierra. Sabía que la distancia entre Alejandría y Siena era de aproximadamente 5.000 estadios (el estadio es una medida de longitud griega cuyo valor cambiaba según época y lugar) y como 7,2 grados representan una cincuentava parte de un círculo completo (360 grados), la circunferencia total de la Tierra debía ser 50 veces esa distancia: 5,000 * 50 = 250,000 estadios

Si Eratóstenes estaba usando el estadio ático, el más normal en su ciudad y época, su resultado sería equivalente a 46,250 Km; y si usó el estadio egipcio, como dicen sus defensores, entonces su resultado sería equivalente a 39,250 Km, frente a los 40,008 Km que son la medida oficial actual; impresionante. Si el primer cálculo os parece un error grande os animo a que salgáis a la calle armados con un compás y un par de cuerdas y midáis el tamaño de la tierra a ver que os sale. Esperamos vuestras respuestas.

¿Qué dificultades tuvo que enfrentar Eratóstenes para su cálculo? Muchas y diversas: supuso que la Tierra es perfectamente esférica cuando no lo es; supuso que Siena y Alejandría están en el mismo merididano (misma longitud) cuando hay unos tres grados de diferencia; la distancia entre Siena y Alejandría desde luego no había sido medida con gran exactitud; Siena no estaba exactamente en el Trópico de Cancer, sino a unos 40 Km en la época de Eratóstenes; y finalmente Eratóstenes no tenía siquiera transportador de ángulos, así que para medir el ángulo de la sombra del obelisco se valdría, probablemente, de un simple compás o el gnomón de un reloj de sol.

- Mira merluzo, si está clarísimo, mides ángulos y ya está.
En serio: Cuadro Eratóstenes enseñando en Alejandría, de Bernardo Strozzi, circa 1635
Imagen del Museo de Bellas Artes de Montreal

En cualquier caso, gracias a Eratóstentes, los griegos ya tenían un dato fundamental: el tamaño (aproximado) del planeta en el que vivían. Y con ese conocimiento, se abría la puerta a más preguntas: ¿podrían calcularse también el tamaño y la distancia a la Luna? ¿Y qué hay del Sol? Para responder a eso, tendríamos que seguir los pasos de otro gran pensador que vivió antes que el propio Eratóstenes: Aristarco de Samos. Pero esa, amigos, es otra historia…